跳跃列表是一种随机数据结构。它使得包含 n 个元素的有序序列的查找、插入、删除操作的平均时间复杂度都是 O(log n)。(注意关键词有序,如果不需要有序,也不需要用到跳跃列表;数据量大时,时间复杂度退化到较慢的概率微乎其微)
| 平均 | 最差 | |
| 搜索 | O(log n) | O(n) |
| 插入 | O(log n) | O(n) |
| 删除 | O(log n) | O(n) |
| 空间 | O(n) | O(n log n) |
跳跃列表是通过维护一个多层的链表实现的。每一层链表中的元素的数量,在统计上来说都比下面一层链表元素的数量更少。也就是说,上层疏,下层密,底层数据是完整的,上面的稀疏层作为索引——这就是链表的“二分查找”啊。
一开始时,算法在最稀疏的层次进行搜索,直至需要查找的元素在该层两个相邻的元素中间。这时,算法将跳转到下一个层次,重复刚才的搜索,直到找到需要查找的元素为止。
Wikipedia 的道理就讲到这里,我不希望把本文写得难懂。说好的一图流就能领悟呢?其实我有点标题党,本文不止一幅图,但是核心的图只有一幅,上图(来自 Wikipedia):
请多次认真观看插入节点的全过程 gif。我看完之后,就觉得自己可以实现出来了(虽然后来实际开发调试了很多次)。
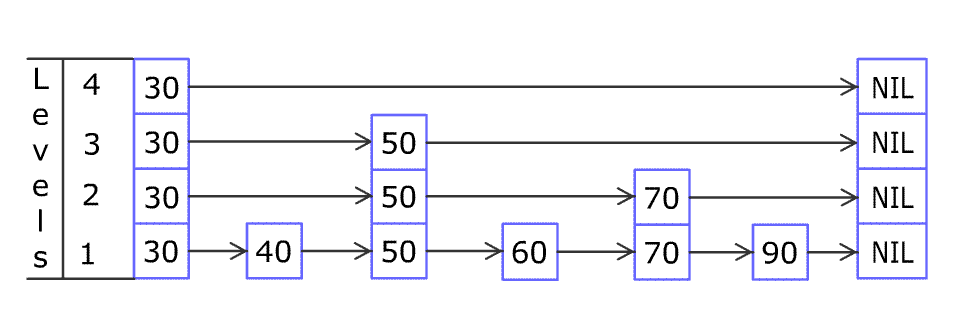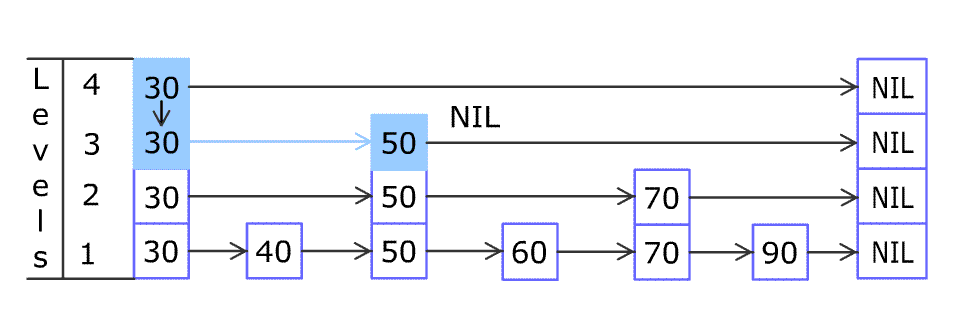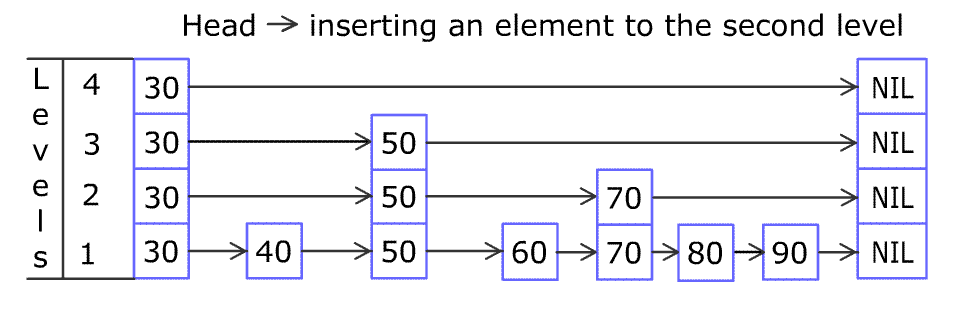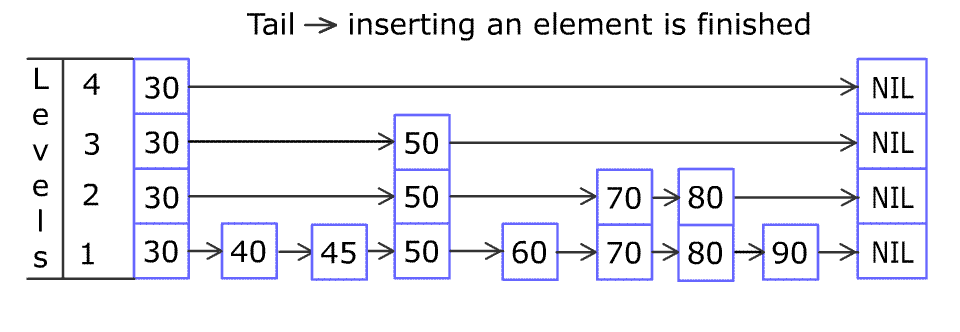
例如想在上图中所示的跳跃列表中插入 80,首先要找到应该插入的位置。
首先从最稀疏的层的 30 开始,把当前位置设置为顶层的 30。
80 比当前位置右边的 NIL 小,所以把当前位置移到下一层的 30;
80 比当前位置右边的 50 大,所以把当前位置右移到 50;
80 比当前位置右边的 NIL 小,所以把当前位置移到下一层的 50;
80 比当前位置右边的 70 大,所以把当前位置右移到 70;
80 比当前位置右边的 NIL 小,所以把当前位置移到下一层的 70;(当前位置已到达底层)
之后用 80 不断与右边的节点比较大小,右移至合适的位置插入 80 节点。(底层插入完毕)
接下来用随机决定是否把这个 80 提升到上面的层中,例如图中的提升概率是 50%(抛硬币),不断提升至硬币为反面为止。
上面一段描述了 gif 中插入 80 的搜索和插入过程。那么,代码如何实现?右移和下移的逻辑很浅显,那么重点就在如何提升节点到上层的逻辑。
为了方便代码的实现,我给每一层链表的头部都定义一个根节点 Root(图中以“R”标识),根节点的值其实没有用到;定义末尾的 NIL 比任意元素都大。每一个节点都有 2 个指针,一个指向右边(next),另一个指向下边(dense)。算法起始的“当前位置”设定在最顶层的 R。
见下图,重温插入 80 的过程,右移和下移的步骤和刚才是一致的,只是左边多了一个 R:从最上层的 R 开始,如果 80 比当前节点右边的值大,那么当前位置右移,否则当前位置下移。一直走到到底层的 70 节点。
找到待插入的位置之后,要在底层(第 1 层)的 70 后面插入 80。
然后,如果要提升一层呢?要在第 2 层的 70 后面插入 80。
如果再提升一层呢?要在第 3 层的 50 后面插入 80。
如果再提升一层呢?要在第 4 层的 30 后面插入 80。
如果再提升一层呢?要新建一个第 5 层,在第 5 层的 R 后面插入 80。
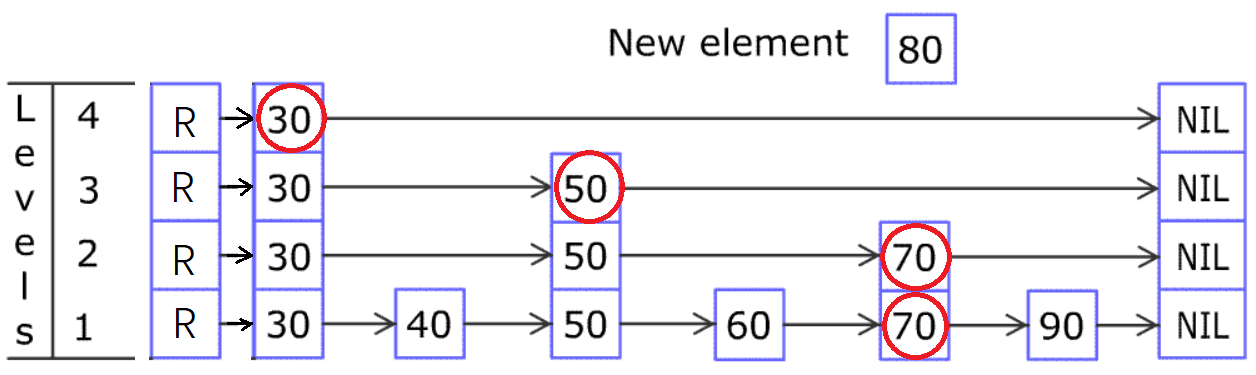
问题来了,怎么知道要在上层的哪个节点后面插入 80?也就是下图的红圈节点是怎么确定的?
.
.
.
如果稍微回味一下,就可以知道:红圈节点都是搜索的时候,决定“下移”的时候当前位置的节点!!(底层的那个除外)
我举另外一个例子,在原图中插入 65,同样除了底层的 60,其余红圈节点都是决定下移的时候的节点。
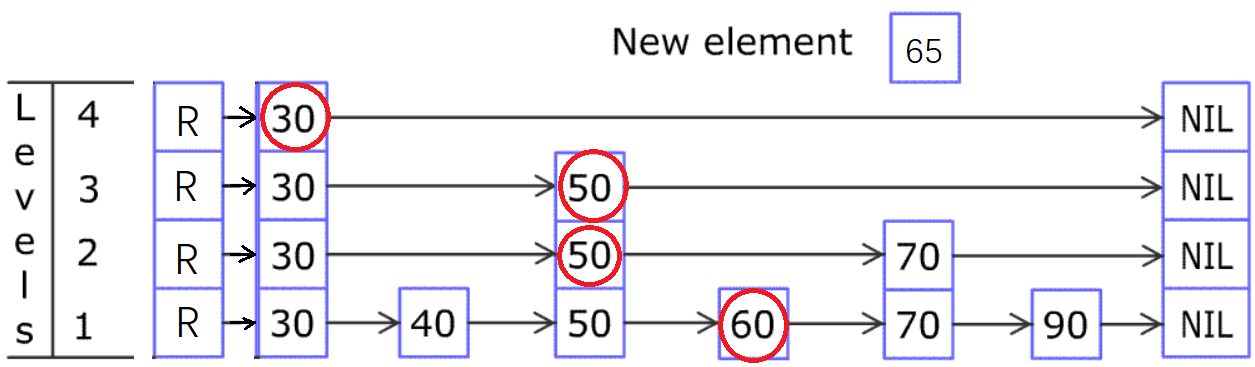
一旦想通了这点,代码就会写了。这就是标题中“领悟”的含义。
搜索时,下移的时候,把当前所处的节点记下来。底层的仅小于待插入值的节点,也记下来。那么插入值为 x 的节点以及提升 x 节点的操作,都是在记录的节点后,分别插入 x 节点。
跳跃列表的插入就讲完了。那么删除呢?
又可以领悟一下。
.
.
我领悟了 10 分钟,一度以为需要加一个向左指的指针,后来发现,并不需要。
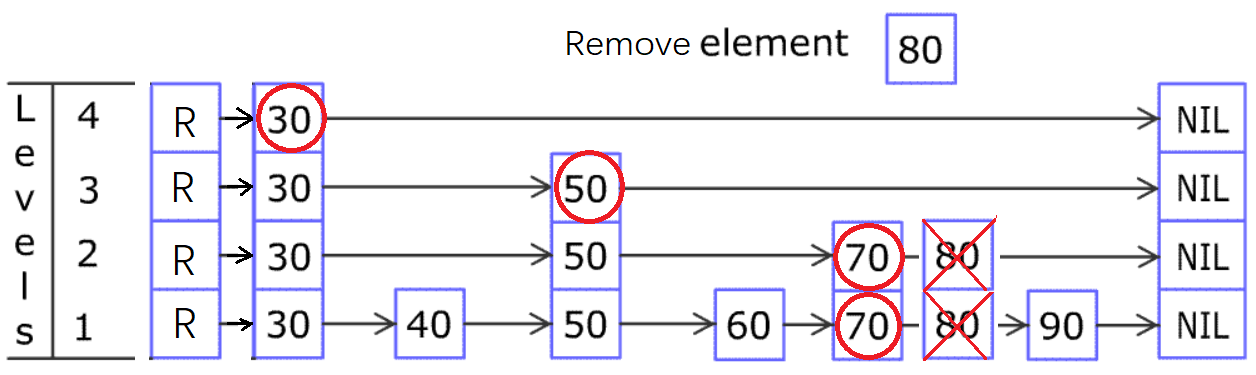
假设要在下图中删除值为 80 的节点,无论 80 节点是只存在于第 1 层,还是已提升了多少层,删除的时候,都是判断红圈节点的右边是不是 80,如果是就把它删掉。
如下图,可以对比上文中插入 80 的图,可以发现红圈节点是一样的。
换成 65 的例子,结论不变:
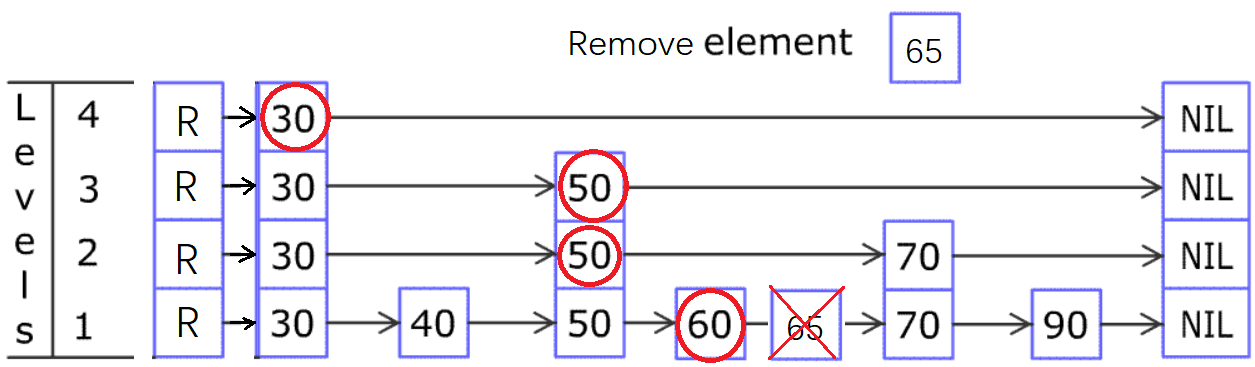
至于删除了节点后,顶层变空,就把该层删掉,没有特别之处。
至此,跳跃列表这个数据结构就领悟完毕,上面的内容无需结合代码来解释。下面直接贴出我的 Python 实现。代码的核心就在_find()方法里,它负责找到标红圈的节点;至于add()和remove()方法,就是对红圈节点做插入和删除操作罢了。
我把在具体调试的代码注释掉了,如果你想手动调试以便理解它运行的过程,可以把 6~11 行注释掉,并解除 15~26、64~72 行的注释,手动调用skip_list.debug()方法,可以打印出各个节点的数值及指向。
Java 和 Kotlin 的实现就不贴在文中了,不然页面太长吓到人,见 GitHub: 我的实现。由于我是先写 Python 再移植的,移植的版本就不写太多注释了。多写两个版本是为了学习 Java 和 Kotlin 语言,可能写得差一点哈。
代码附带了简单的性能测试。在我的电脑上,以 MAX = 999999999 和 LENGTH = 100000 测试,Python 版add耗时约 1.1s,remove耗时约 1s;Kotlin 版add耗时约 0.3s,remove耗时约 0.15s,Java 版耗时相似。Python 的性能没有想象中弱,原来预计要慢一个数量级。
import random
import time
from typing import List
class Node:
__slots__ = ('value', 'next', 'dense')
def __init__(self, value, next = None):
self.value = value
self.next: Node = next
self.dense: Node = None # 指向更底层的同值节点
# 给每个Node编号,方便debug
# class Node:
# number = 1
# def __init__(self, value, next = None):
# self.id = Node.number
# Node.number += 1
# self.value = value
# self.next: Node = next
# self.dense: Node = None # 指向更底层的同值节点
# def __repr__(self):
# return f'(#{self.id}, value: {self.value}, ' \
# f'→: #{self.next.id if self.next else None}, ↓: #{self.dense.id if self.dense else None})'
class SkipList:
"""
使用跳表维护一个 查找(判断存在性)、添加、删除 的平均时间都是O(log n)的 自排序链表
实际上是多层的链表,底层是完整的链表,越上层的链表越稀疏
"""
def __init__(self, promote_probability=0.5):
self._size = 0
self._promote_probability = promote_probability
self.roots: List[Node] = [Node(None)] # 初始为1层root节点,root节点的值没有用到,可填None
def __len__(self):
return self._size
def __str__(self):
return str(self.to_list())
def __repr__(self):
return str(self)
def to_list(self):
""" 只返回底层密链表的数据 """
result = []
node = self.roots[0].next
while node:
result.append(node.value)
node = node.next
return result
def __contains__(self, val):
memory_nodes = self._find(val)
if memory_nodes[-1].next.value == val:
return True
return False
# def debug(self):
# for root in self.roots[::-1]:
# result = []
# node = root.next
# while node:
# result.append(repr(node))
# node = node.next
# print(result)
# print()
def _insert_node(self, new_node: Node, prev: Node):
""" 使
prev -> prev_next
变成
prev -> new_node -> prev_next
"""
original_next = prev.next
new_node.next = original_next
prev.next = new_node
def _remove_node(self, to_remove: Node, prev: Node):
""" 使
prev -> to_remove -> to_remove_next
变成
prev -> to_remove_next
"""
prev.next = to_remove.next
del to_remove
def _find(self, val) -> List[Node]:
""" 由顶层的root节点向较密层搜索给定的val,并由顶至底记录标红的节点 """
memory_nodes: List[Node] = []
i = len(self.roots) - 1 # 顶层的root节点
current_node = self.roots[i]
# 搜索高层的节点,记录往下移动的节点
while i > 0:
while current_node.next and val > current_node.next.value:
current_node = current_node.next
memory_nodes.append(current_node)
current_node = current_node.dense
i -= 1
# 搜索底层的节点,记录刚好小于val的节点
while current_node.next and val > current_node.next.value:
current_node = current_node.next
memory_nodes.append(current_node)
return memory_nodes
def add(self, val):
# print('add', val) ################################ debug
self._size += 1
# 找到标红的节点
memory_nodes = self._find(val)
# 首先在底层插入节点,这是100%插入的
new_node = Node(val)
self._insert_node(new_node=new_node, prev=memory_nodes.pop()) # 从底层开始pop
current_node = new_node
# 然后随机决定是否向上层添加相同值节点作为索引
current_level = 1 # 底层的level是0,1即上一层
while random.random() < self._promote_probability:
# 新建节点,确定dense的指向
upper_node = Node(val)
upper_node.dense = current_node
current_level += 1
if current_level <= len(self.roots): # 不用加新的层,在之前搜索的节点之后添加节点
self._insert_node(new_node=upper_node, prev=memory_nodes.pop())
else: # 加新的层有2个节点: root节点 -> 新节点(upper_node) -> None
new_root_node = Node(None, next=upper_node) # 新的root节点
new_root_node.dense = self.roots[current_level-2]
self.roots.append(new_root_node)
break
current_node = upper_node
def remove(self, val):
""" 找到标红的节点,然后检查这些节点的next是否等于val,相等则删除,并处理可能的空层 """
if val not in self:
raise ValueError(f'{val} not in this skip list')
memory_nodes = self._find(val)
for node in memory_nodes: # 从上层往下层
if node.next and node.next.value == val:
self._remove_node(node.next, node)
self._size -= 1
# 从上层往下层,检查是否有层被清空,有则把该层的root节点也清除,底层的除外
for i in range(len(self.roots)-1, 0, -1):
if self.roots[i].next is None:
self.roots.pop(i)
if __name__ == "__main__":
MAX = 999999999
LENGTH = 100000
# random.seed(1234)
skip_list = SkipList(promote_probability=0.5)
test_data = [random.randint(1, MAX) for _ in range(LENGTH)]
t1 = time.perf_counter()
for num in test_data:
skip_list.add(num)
t2 = time.perf_counter()
# skip_list.debug() # 可以debug看一下
test_data_sorted = sorted(test_data)
print('correct:', str(test_data_sorted) == str(skip_list))
print('add time cost:', t2-t1)
##############################
t3 = time.perf_counter()
data_to_remove = test_data[:LENGTH//2] # 抽前面一半的数来删除
for num in data_to_remove:
skip_list.remove(num)
t4 = time.perf_counter()
test_data_remaining_sorted = sorted(test_data[LENGTH//2:])
print('correct:', str(test_data_remaining_sorted) == str(skip_list))
print('remove time cost:', t4-t3)
# LENGTH比较大的话,下面相当慢
# print('=============================================')
# def insert_to_list(_list: list, val):
# """ 按大小插入列表,保证插入前和插入后列表均有序 """
# if not _list:
# _list.append(val)
# else:
# i = 0
# length = len(_list)
# while i <= length - 1 and _list[i] < val:
# i += 1
# _list.insert(i, val)
# python_list = []
# t5 = time.perf_counter()
# for num in test_data:
# insert_to_list(python_list, num)
# t6 = time.perf_counter()
# print('correct:', str(test_data_sorted) == str(python_list))
# print('add time cost slow version:', t6-t5)
相关参考
- Wikipedia:https://en.wikipedia.org/wiki/Skip_list
- Redis sorted sets:https://redis.io/topics/data-types#sorted-sets,也用到了跳跃列表
- GitHub: 我的实现
发表评论